柱面透镜可用于单轴会聚或发散光束,在光学测量、激光扫描、光谱学、激光二极管输出光束整形、X射线光显微成像等诸多行业和领域都有广泛应用的应用程序。
将准直射光源变为线光源
L = 2(r0/f)(z+f)
L = 2 (r0 / f) (z + f)
当z大于f时,膨胀比接近z/f,线长与z成正比。
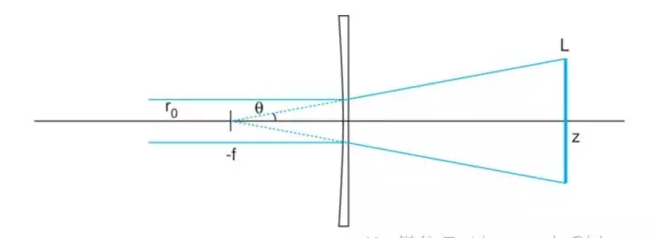
如果需要在z产生宽度很窄的线光源,可以在平面凹柱面透镜前端或平凸柱面透镜后端的焦距为z,与平面凹柱面透镜正交,以压缩光束宽度。
二极管输出准直光束
激光二极管输出光束以不对称形式发散,其准直接工作更具挑战性。例如,发散角θ。 Theta 1 x 2 = 10° x 40° 二极管光源,如果只使用标准 球面透镜 ,只有在一个方向准直时,才会发生另一个方向的发散或收敛。使用将问题分解为两个一维方向的柱面透镜,通过两个正交柱面透镜的组合,可以同时准直两个方向。
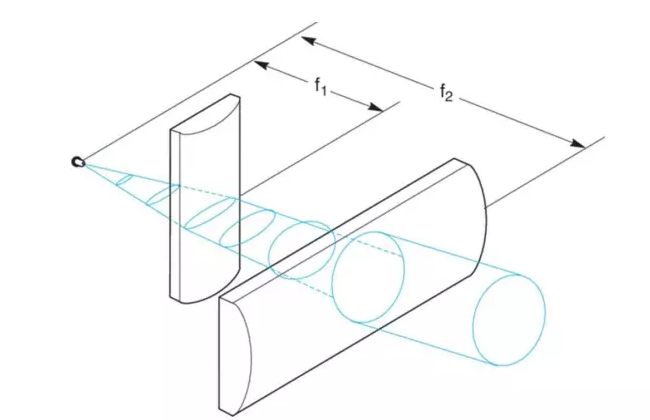
柱面透镜的选择和光路的安装应遵循以下规则:
θ1/θ2 = 10°/40° = f1/f2
1)调整后使光斑对称,两个柱面透镜的焦距比等于发散角。
Theta 1 / theta 2 = 10°/ 40° = f1 / f2
2)激光二极管可以近似为一个点光源,得到准直输出,两个圆柱体与光源的间距等于两者的焦距。
3)两柱面主平面间距应等于f2-f1焦距之差,两透镜实际间距等于BFL2-BFL1。与球面透镜一样,柱面镜的凸面应朝向准直射光束,以尽可能减少。
d1 = 2f1(tan(θ2/2))
d2 = 2f2(tan(θ1/2))
4)由于激光二极管输出光束发散较快,我们需要仔细确认每个圆柱上的光斑尺寸不超过镜头的有效光孔径。因为圆柱的距离等于它的焦距,所以每个圆柱的最大光斑宽度应遵循
D1 = 2f1 (theta 2/2)
D2 等于 2f2,θ 的正切的二分之一。
例如Newport CKX012 (f1 = 12.7 mm, BFL1 = 7.49 mm)和CKX050 (f2 = 50.2 mm, BFL2 = 46.03 mm)柱面透镜的组合,两个透镜在平面上的间距为BFL2 - BFL1 = 38.54毫米。第一个柱面透镜的光斑直径为
D1 = 2 (12.7 毫米) 棕褐色 (20°) = 9.2 毫米
第二个圆柱体中的光斑直径为
D2 = 2 (50.2 毫米) 棕褐色 (5°) = 8.8 毫米
虽然还有一点不对称,但是这两个柱面透镜的简单组合,大大提高了光束的质量。
 Call us on:
Call us on:  Email us:
Email us:  产研中心:南京市雨花区青年路1号联东u谷雨花国际智慧谷 9B-401
产研中心:南京市雨花区青年路1号联东u谷雨花国际智慧谷 9B-401









 中文
中文  EN
EN
 de
de  es
es  fr
fr 


